Baizer

Balanced Binary Search Tree ​

平衡二叉搜索树 ​

二叉搜索树的缺陷：二叉搜索树在极端情况下，如果每次插入的数据都是最小或者都是最大的元素，那么树结构会退化成链表，二叉树时间复杂度也将从O(logn)退化为 O(n)。

解决方案：在节点的添加、删除操作之后，想办法让二叉搜索树恢复平衡（减小树的高度）——自平衡

常见的平衡二叉搜索树：AVL树、红黑树

AVL Tree ​

AVL树（取名源自两位发明者的名字： G. M. Adelson-Velsky 和 E. M. Landis ，苏联的科学家）

在二叉查找树的基础上加上限制，保证让每个节点的左右子树高度差不能超过 1，那么这样让可以让左右子树都保持平衡，使其时间复杂度保持为 O(logn)。

平衡因子（Balance Factor） ​

  • 指某节点的左右子树的高度差（即节点左子树的高度减去右子树的高度）

  • 每个节点的平衡因子只可能是 1、0、-1（绝对值 ≤ 1，如果超过 1，称之为 “失衡"）

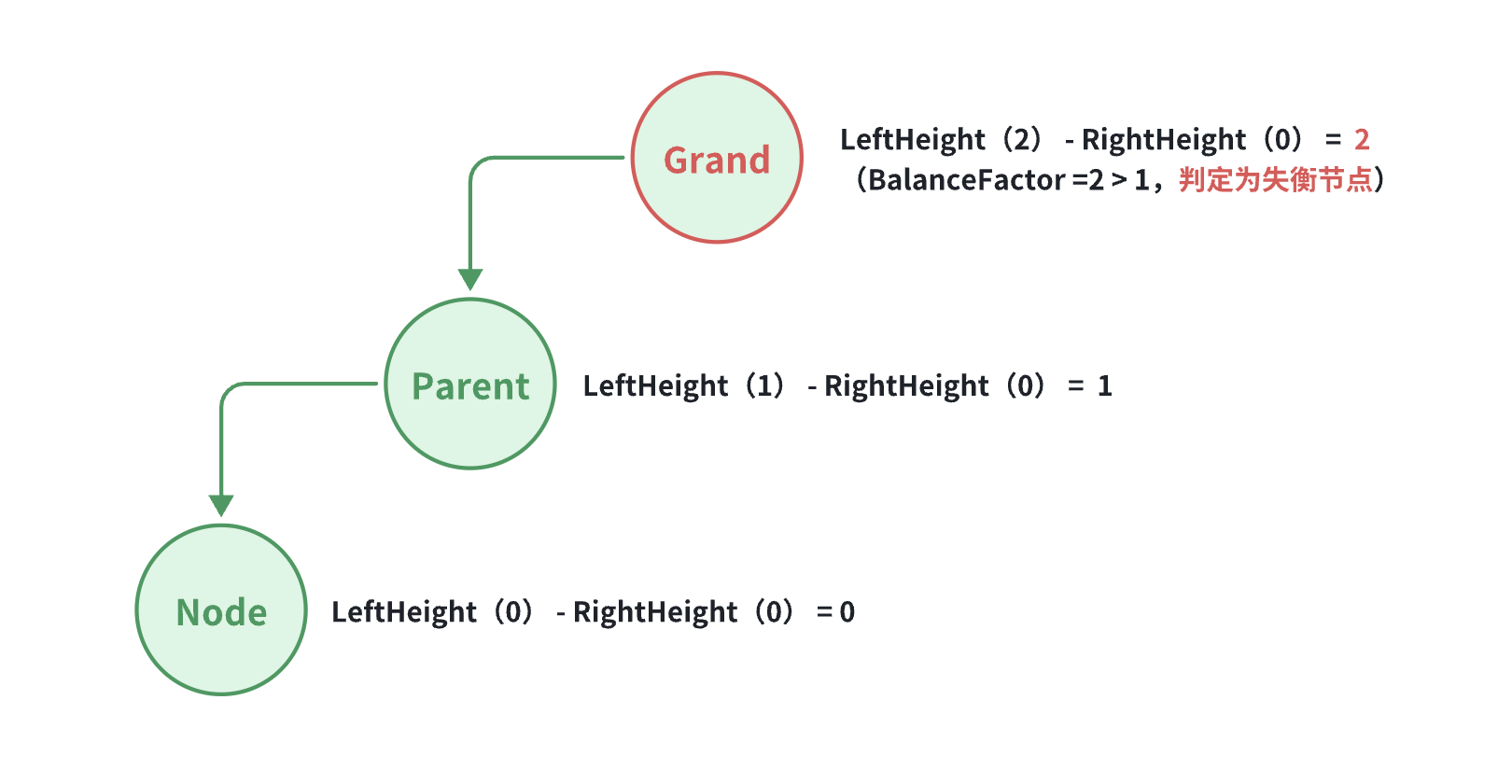
image-20250107210333123

失衡的四种情况 ​

注意：Child节点可能为null节点。

  • LL = left - left：Grand.left.left节点有添加，导致的失衡
  • RR = right - right

Grand的最高子节点 = Parent，Parent的最高子节点 = Node，以下四种情况涵盖了所有失衡节点的情况。

LL失衡：右旋转 ​

image-20250107210541663

RR失衡：左旋转 ​

image-20250107210859933

LR失衡：先左旋转，再右旋转 ​

image-20250107210918458

转换为 LL 的情况之后，再按上方 LL 失衡情况处理。

RL失衡：先右旋转，再左旋转 ​

image-20250107210932660

转换为 RR 的情况之后，再按上方 RR 失衡情况处理。

代码实现 ​

Node节点的扩展 ​

新增isLeftChild、isRightChild、balancefactor、isBalanced、updateHight、tallerChild方法，height属性

  • 注意：节点高度默认为1
java
/**
 *  树节点 基本构造
 * 
 * @author XRZ
 */
public class Node<E> {

    public E element;
    public Node<E> parent;  //AVL树、红黑树中使用
    public Node<E> left;
    public Node<E> right;

    public Node(E element, Node<E> parent) {
        this.element = element;
        this.parent = parent;
    }

    public boolean isLeaf() {
        return left == null && right == null;
    }

    public boolean hasTwoChildren() {
        return left != null && right != null;
    }

    public boolean isLeftChild(){
        return parent != null && this == parent.left;
    }

    public boolean isRightChild(){
        return parent != null && this == parent.right;
    }


    //===================【供AVL树使用】

    public int height = 1; //节点高度默认为1

    /**
     * 平衡因子（Balance Factor）
     *      指某节点的左右子树的高度差（即节点左子树的高度减去右子树的高度）
     *      每个节点的平衡因子只可能是 1、0、-1（绝对值 ≤ 1，如果超过 1，称之为 “失衡"）
     *
     * @return
     */
    public int balancefactor(){
        int leftHeight = this.left == null ? 0 : this.left.height;
        int rightHeight = this.right == null ? 0 : this.right.height;
        return leftHeight - rightHeight;
    }

    /**
     * 判断是否为平衡节点（平衡因子绝对值不能超过1）
     *      绝对值：负数将会被转换为正数返回
     * @return
     */
    public boolean isBalanced(){
        return Math.abs(this.balancefactor()) <= 1;
    }

    /**
     * 更新当前节点高度
     */
    public void updateHight(){
        int leftHeight = this.left == null ? 0 : this.left.height;
        int rightHeight = this.right == null ? 0 : this.right.height;
        height = 1 + Math.max(leftHeight,rightHeight);
    }

    /**
     * 获取最高的子节点
     * @return
     */
    public Node<E> tallerChild(){
        int leftHeight = this.left == null ? 0 : this.left.height;
        int rightHeight = this.right == null ? 0 : this.right.height;

        if(leftHeight > rightHeight) return this.left;
        if(rightHeight > leftHeight) return this.right;

        // 相同高度时，返回相同方向的子节点
        return this.isLeftChild() ? this.left : this.right;
    }
}

afterAdd() ​

添加节点之后调整，确保树的平衡。

  • 获取添加的节点，向上寻找其失衡的父节点。

  • 找到第一个失衡的父节点（Grand节点）修复它，其余的父节点也就恢复了。

java
/**
 * 添加节点之后调整，确保树的平衡
 * @param node
 */
public void afterAdd(Node<E> node){
    // 向上循环，寻找第一个失衡的父节点
    while((node = node.parent) != null){

        if(node.isBalanced()){
            //平衡节点，更新高度即可
            node.updateHight();
        }else{
            //失衡节点，需要重新恢复平衡
            this.rebalance(node);
            break; //第一个失衡的父节点恢复后，所有失衡的父节点也就恢复了，直接退出
        }
    }
}

恢复平衡 rebalance() ​

java
/**
 * 恢复平衡
 *
 * @param grand 失衡节点
 */
private void rebalance(Node<E> grand) {
    // Grand的最高子节点 = Parent，Parent的最高子节点 = Node
    Node<E> parent = grand.tallerChild();
    Node<E> node = parent.tallerChild();

    // 以下四种情况涵盖了所有失衡节点的情况。
    if (parent.isLeftChild()) {
        if (node.isLeftChild()) {
            // LL失衡
            this.rotateRight(grand); // 右旋转解决
        } else {
            // LR失衡
            this.rotateLeft(parent); // 先把Parent左旋转，成为LL
            this.rotateRight(grand); // 再把Grand右旋转解决
        }
    } else {
        if (node.isRightChild()) {
            // RR失衡
            this.rotateLeft(grand); // 左旋转解决
        } else {
            // RL失衡
            this.rotateRight(parent); // 先把Parent右旋转，成为RR
            this.rotateLeft(grand);   // 再把Grand左旋转解决
        }
    }
}

右旋转 rotateRight() ​

java
/**
 * 右旋转
 *
 * @param grand 失衡节点
 */
public void rotateRight(Node<E> grand) {
    Node<E> parent = grand.left;   // 以parent为原点，把grand往右旋转
    Node<E> childA = parent.right; // 相当于示例图中的A节点

    // 更新grand、parent的子节点
    parent.right = grand;
    grand.left = childA;

    //==========下方代码与左旋转一致

    //维护原失衡节点的父节点
    Node<E> childRoot = grand.parent;
    if (grand.isLeftChild()) childRoot.left = parent;
    else if (grand.isRightChild()) childRoot.right = parent;
    else
        super.root = parent;    //没有父节点，说明grand是root节点


    // 更新grand、parent、child的父节点
    parent.parent = childRoot;
    grand.parent = parent;
    if (childA != null) {
        childA.parent = grand;
    }

    // 更新grand、parent的高度
    grand.updateHight();
    parent.updateHight();
}

左旋转 rotateLeft() ​

java
/**
 * 左旋转
 *
 * @param grand 失衡节点
 */
public void rotateLeft(Node<E> grand) {
    Node<E> parent = grand.right;  // 以parent为原点，把grand往左旋转
    Node<E> childA = parent.left;  // 相当于示例图中的A节点

    // 更新grand、parent的子节点
    parent.left = grand;
    grand.right = childA;

    //==========下方代码与右旋转一致

    //维护原失衡节点的父节点
    Node<E> childRoot = grand.parent;
    if (grand.isLeftChild()) childRoot.left = parent;
    else if (grand.isRightChild()) childRoot.right = parent;
    else
        super.root = parent;    //没有父节点，说明grand是root节点


    // 更新grand、parent、child的父节点
    parent.parent = childRoot;
    grand.parent = parent;
    if (childA != null) {
        childA.parent = grand;
    }

    // 更新grand、parent的高度
    grand.updateHight();
    parent.updateHight();
}

afterRemove() ​

删除之后失衡的处理

参考 ​