Back Tracking 回溯
核心概念
回溯(Back Tracking)
回溯可以简单理解为:通过选择不同的岔路口来通往目的地(找到想要的结果)
- 每一步都选择一条路出发,能进则进,不能进则退回上一步(回溯),换一条路再试
树的前序遍历、图的深度优先搜索(DFS)、八皇后、走迷宫都是典型的回溯应用。
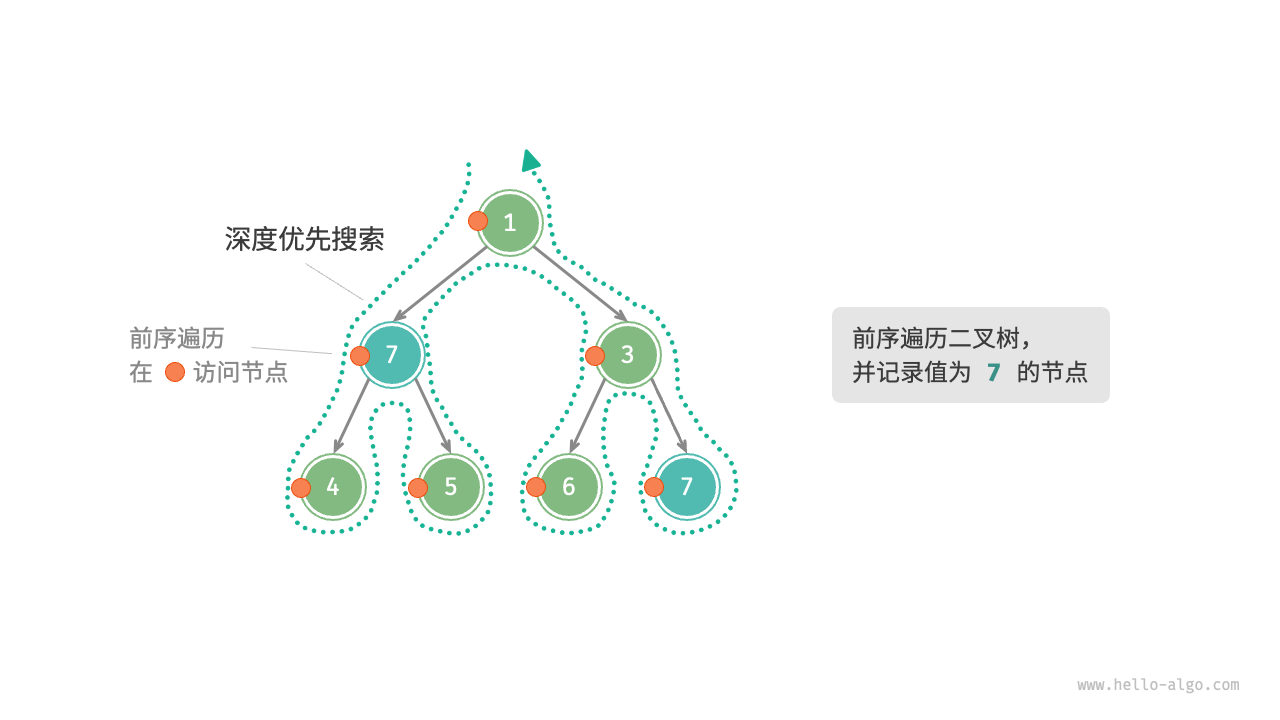
剪枝(pruning)
复杂的回溯问题通常包含一个或多个约束条件,约束条件通常可用于“剪枝”。
“剪枝”是一个非常形象的名词。在搜索过程中,可以“剪掉”不满足约束条件的搜索分支,避免许多无意义的尝试,从而提高搜索效率。
- 例如,在上图的搜索动作中增加一个条件:要求路径中不包含值为 3 的节点

八皇后(Eight Queens)
八皇后问题是一个古老而著名的问题
- 在8x8格的国际象棋上摆放八个皇后,使其不能互相攻击:任意两个皇后都不能处于同一行、同一列、同一斜线上。
请问有多少种摆法?
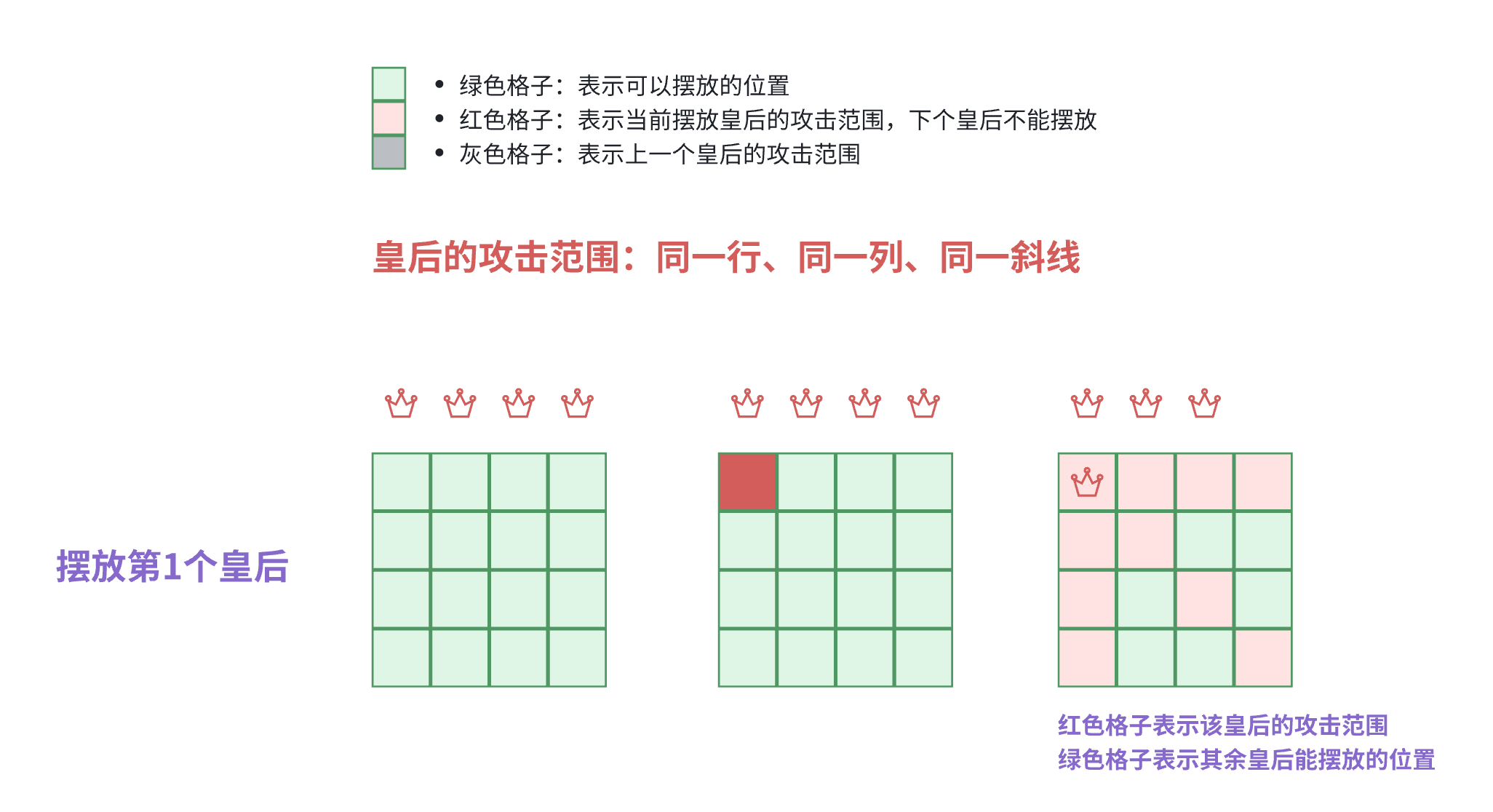
四皇后
为方便理解,缩小数据规模,把八皇后改为四皇后:4X4的棋盘上,摆放4个皇后。
摆放第2个皇后
在绿色格子中选择摆放第二个皇后,并生成对应的攻击范围。
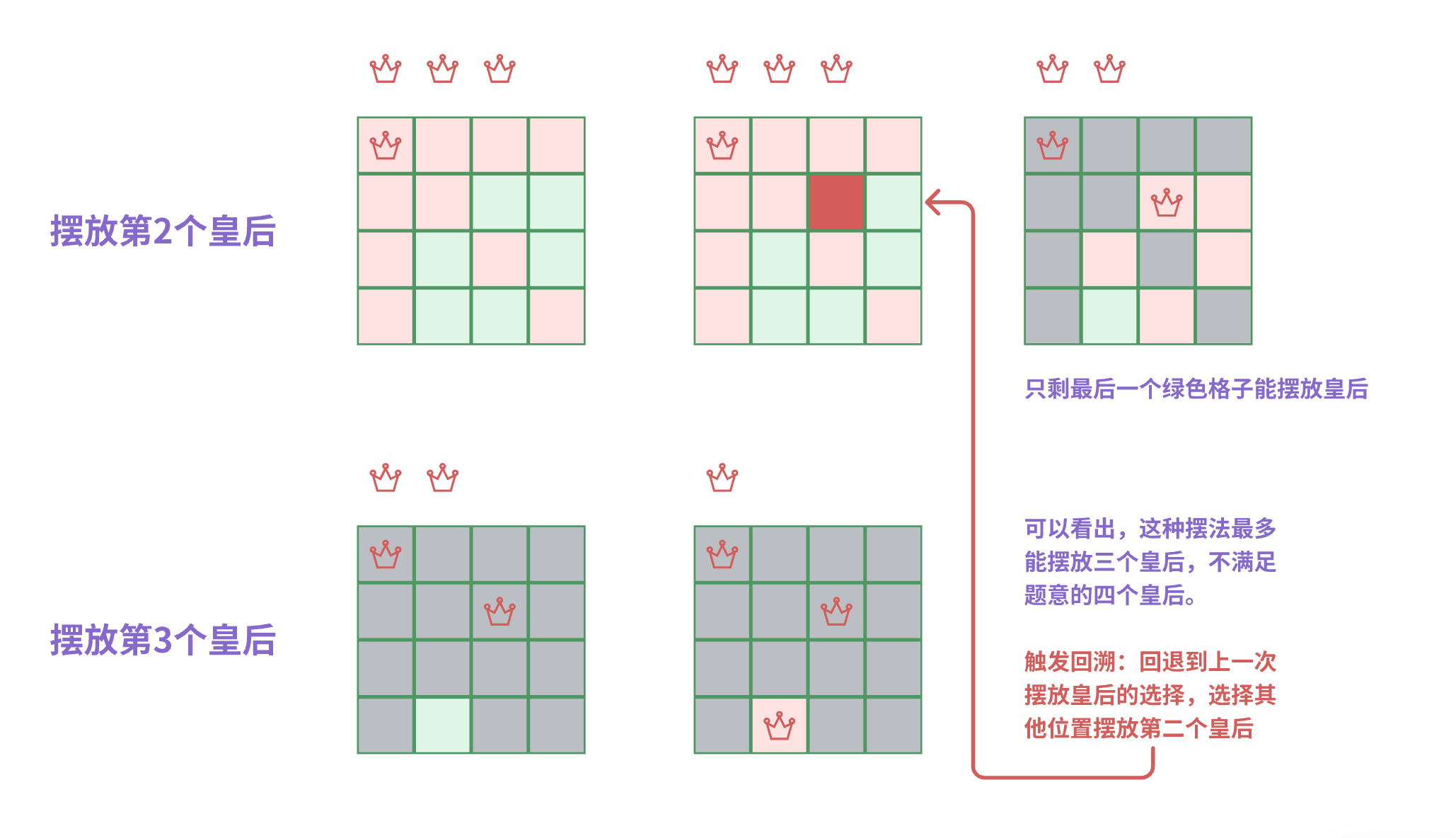
可以看出,这种摆法无论怎么摆,最多能摆放三个皇后,不满足题意的四个皇后。
- 触发回溯:回退到上一次摆放皇后的选择,选择其他位置摆放第二个皇后
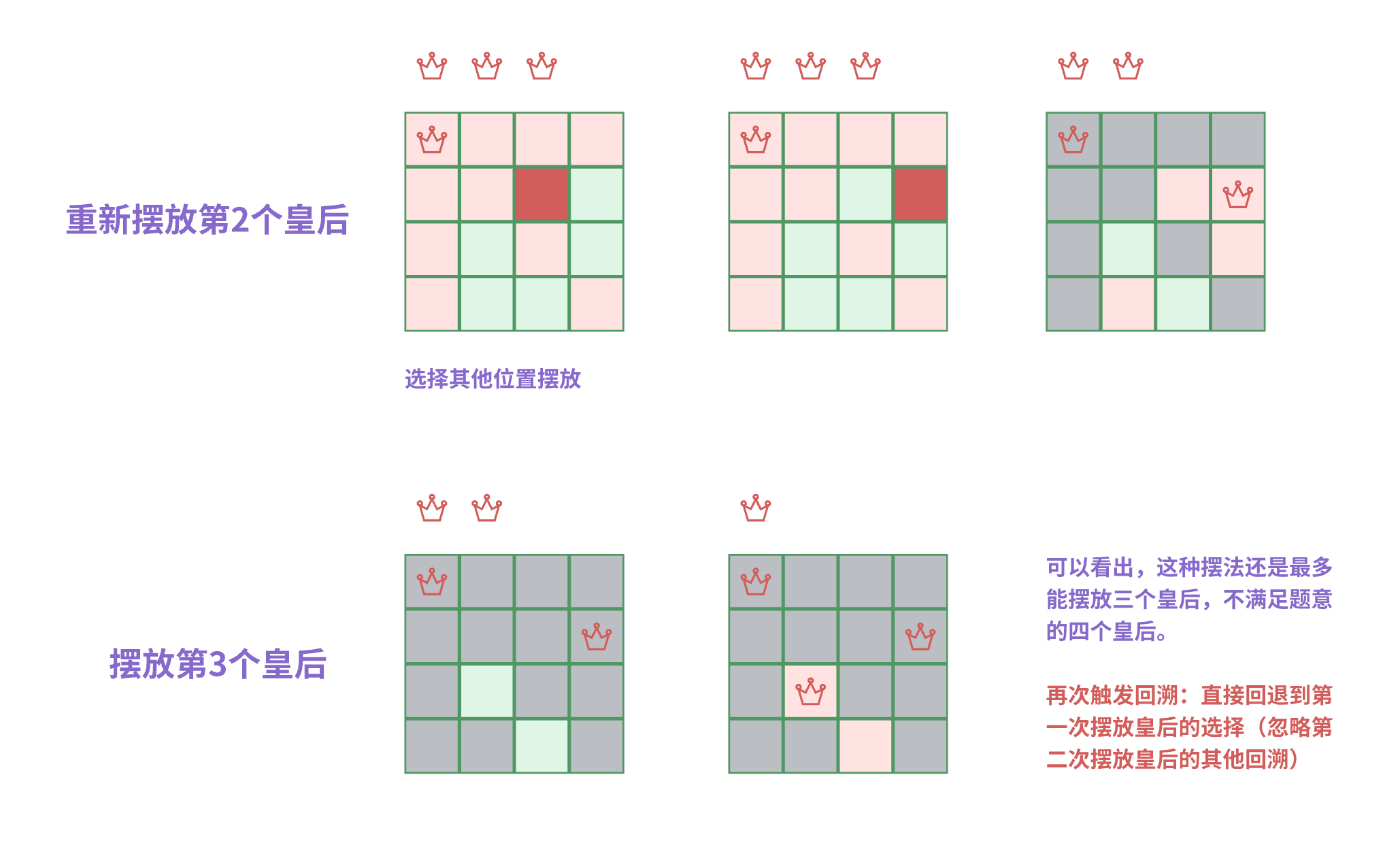
重新摆放第1个皇后
重新选择第二个皇后的位置后发现,无论后续怎么摆,依旧只能最多只能摆三个皇后
- 继续回溯,回退到第一次摆放皇后,重新选择第一次摆放皇后的位置
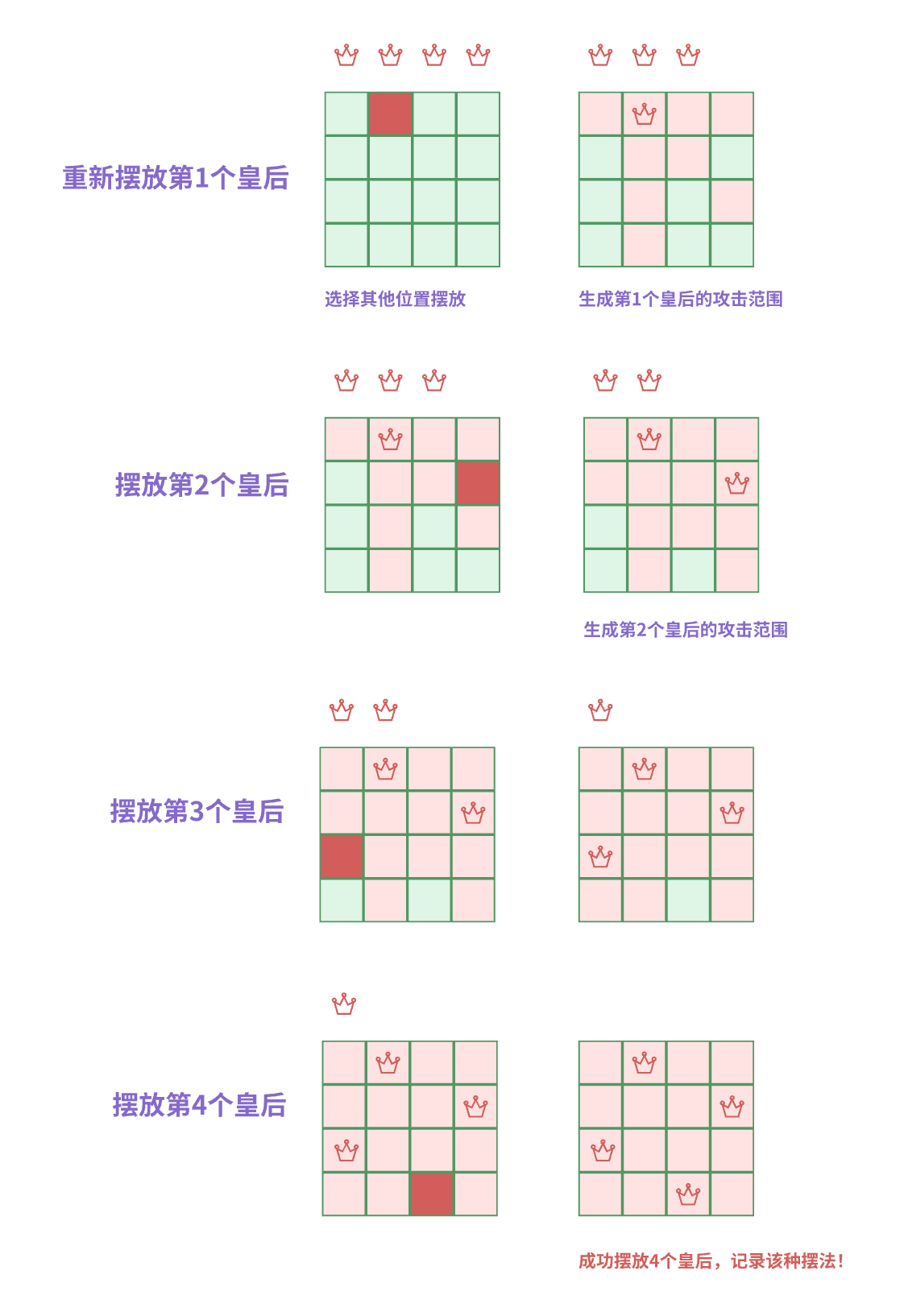
可以看出,这种摆法成功在 4x4 的棋盘上摆放了四个皇后,满足题意,记录该种摆法!
代码实现
棋盘斜线概念
实现前先来了解一下斜线的概念:皇后的攻击范围除了同一行、同一列上,还有同一斜线(又区分为左斜线、右斜线)
- 同一行、同一列就是对应的行号、列号,那么对应斜线呢?
- 如图所示:4x4 的棋盘总共有7条斜线
- 得出斜线条数计算公式:
(n << 1) - 1
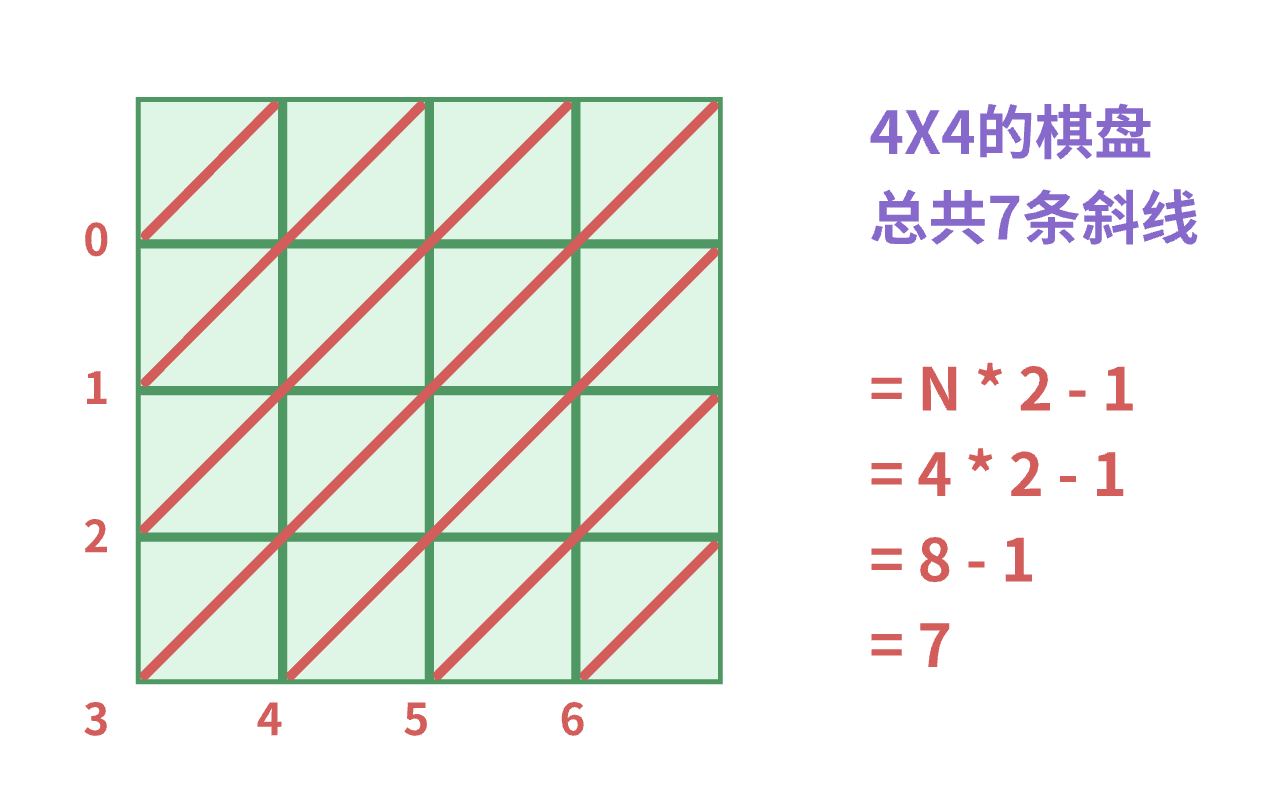
计算出了斜线条数后,如何计算当前位置是在棋盘上的第几条斜线呢?
- 皇后的攻击范围除了上下左右,还包含对角斜线,所以需要判断当前位置在几条斜线上?
- 进一步再判断当前位置的斜线上有没有皇后?如果有,则当前格子位置不能摆放皇后,继续判断下一个格子。
示例:计算当前位置[2,1]在棋盘的第几条右斜线
- 计算公式:
当前行 + 当前列
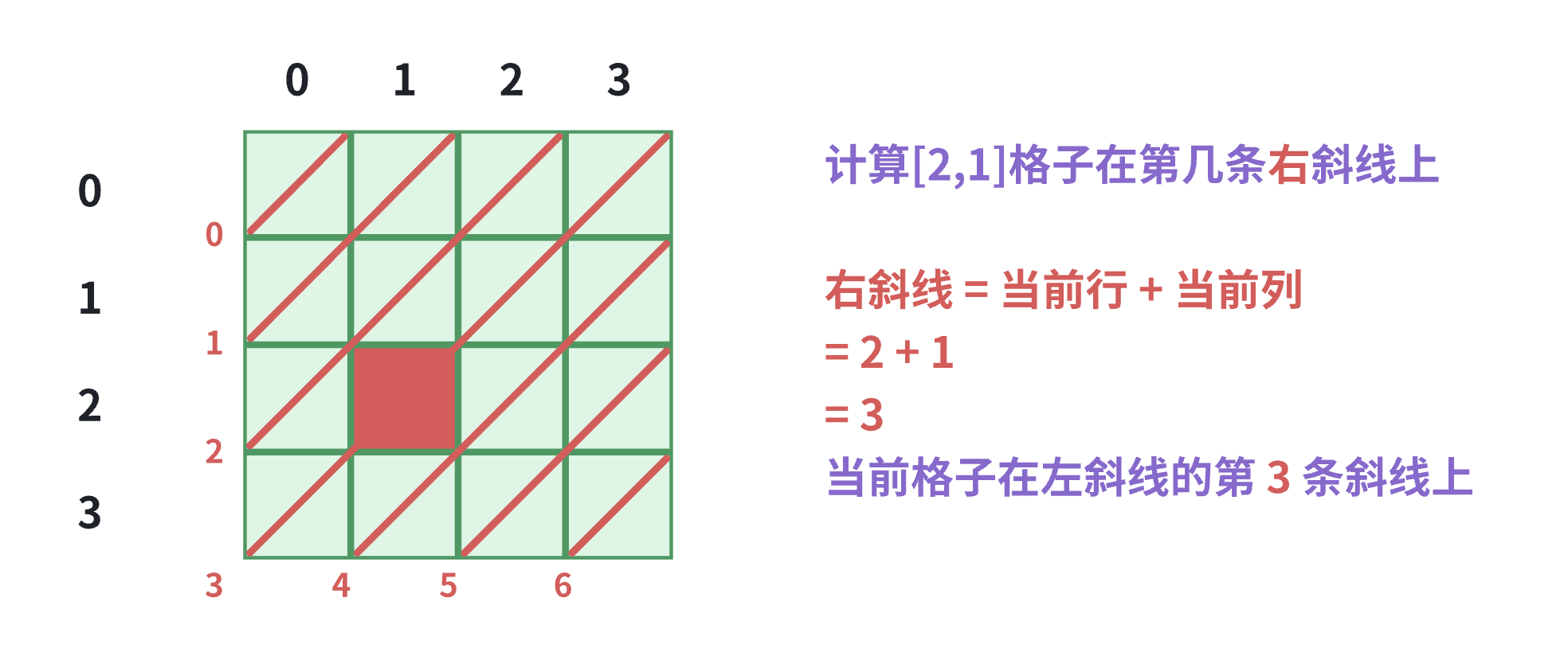
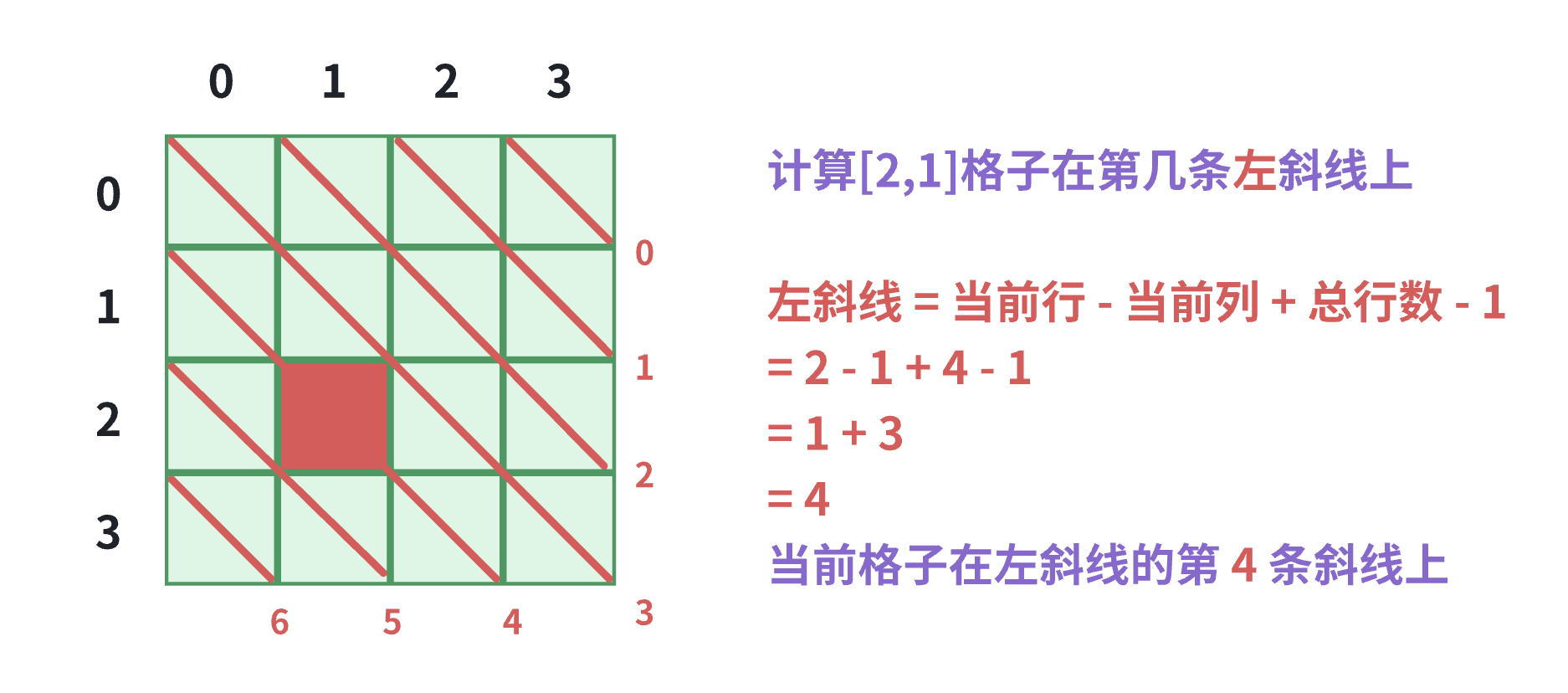
示例:计算当前位置[2,1]在棋盘的第几条左斜线
- 计算公式:
当前行 + 当前列 + 总行数 - 1
完整代码实现
不管是四皇后还是八皇后,在代码中我们直接抽象为N,即入参为N皇后
java
@Test
public void test(){
System.out.println("四皇后的摆法:"+new EightQueensTest().placeQueens(4));
System.out.println("八皇后的摆法:"+new EightQueensTest().placeQueens(8));
}
public int placeQueens(int n){
if(n < 1) return 0;
/**
* 初始化变量
* - 8皇后的话就是8X8的棋盘,皇后最多放置8列,N皇后就是N列。
* - 位运算:(n << 1) 左位移一位 = N * 2
* - 斜线的条数 = N * 2 - 1,即如果是 8X8 的棋盘,共有15条斜线。
*/
cols = new boolean[n];
leftTop = new boolean[(n << 1) - 1];
rightTop = new boolean[(n << 1) - 1];
// 开始摆放皇后,从0行位置开始摆放
this.place(0);
return ways;
}
boolean[] cols; //记录每列是否有皇后:cols[1] = ture 表示第2列有皇后了
boolean[] leftTop; //记录每条斜线是否有皇后(左斜线)[ ↘ ]
boolean[] rightTop; //记录每条斜线是否有皇后(右斜线)[ ↙ ]
int ways = 0; //记录摆放的次数
public void place(int row){
//=== 终止递归条件:每种摆法最少摆N个皇后(cols.length = n)
if(row == cols.length){
// 表示每行都摆了一个皇后(满足题意)
// 例:8皇后即8行8列,如果摆到第8行(实际下标为7),则表示该种摆法满足题意
ways++;
return;
}
//=== 循环每一列,尝试所有摆法
for (int i = 0 ; i < cols.length; i++){
//=== 剪枝:判断当前格子是否可以摆放皇后
// 判断当前i列是否有皇后(每列只能放一个皇后)
if(cols[i]) continue; // 第i列已经有皇后
// 判断当前位置左右斜线是否有皇后
/**
* 先计算当前格子在第几条斜线上
*
* 左斜线 = 当前行 - 当前列 + 总行数 - 1
* 右斜线 = 当前行 + 当前列
*/
int leftIndex = row - i + cols.length - 1;
int rightIndex = row + i;
if(leftTop[leftIndex]) continue; //当前格子的左斜线有皇后
if(rightTop[rightIndex]) continue;//当前格子的右斜线有皇后
//=== 可以摆放,放置皇后,记录位置
cols[i] = leftTop[leftIndex] = rightTop[rightIndex] = true;
//=== 递归下一行(每行只能放一个皇后)
place(row + 1);
//=== 触发回溯:每一次 i++ 就是回溯操作
// 回溯后需要清空记录,还原皇后
cols[i] = leftTop[leftIndex] = rightTop[rightIndex] = false;
}
}改造:打印出皇后位置
增加queens属性和print()方法
java
int[] queens; //记录每行每列皇后的位置(用于打印)
public void placeQueensPrint(int n){
if(n < 1) return;
queens = new int[n];
cols = new boolean[n];
leftTop = new boolean[(n << 1) - 1];
rightTop = new boolean[(n << 1) - 1];
this.placePrint(0);
}
public void placePrint(int row){
if(row == cols.length){
ways++;
this.print(); // 打印当前摆法
return;
}
for (int i = 0 ; i < cols.length; i++){
if(cols[i]) continue;
int leftIndex = row - i + cols.length - 1;
int rightIndex = row + i;
if(leftTop[leftIndex]) continue;
if(rightTop[rightIndex]) continue;
queens[row] = i; //记录 row 行皇后的位置在 i
cols[i] = leftTop[leftIndex] = rightTop[rightIndex] = true;
placePrint(row + 1);
cols[i] = leftTop[leftIndex] = rightTop[rightIndex] = false;
}
}
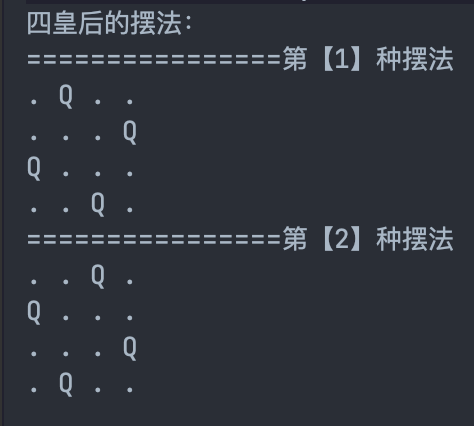
private void print() {
System.out.println("================第【"+ways+"】种摆法");
for (int row = 0; row < cols.length; row++){
for (int col = 0; col < cols.length; col++){
if(queens[row] == col){ // 遍历所有格子,皇后位置打印Q
System.out.print("Q ");
}else{
System.out.print(". ");
}
}
System.out.println();
}
}效果如下: